Définitions

Image by Pete Linforth from Pixabay
Graphe non orienté
Définition
On appelle Graphe non orienté la donnée d'un ensemble $G= (S,A)$ où $S$ est un ensemble fini non vide dont les éléments sont appelés sommets et $A$ est un multi-ensemble fini de paires non ordonnées d'éléments de $S$ appelées arêtes.
Propriétés
Le nombre de sommets est appelé l'ordre du graphe et le nombre d'arêtes est appelé la taille du graphe.
Dans la représentation graphique habituelle, les sommets sont représentés par des cercles et les arêtes par des traits.
Une arête reliant, assommé lui-même est appelée une boucle.
Un graphe est dit simple s'il ne contient pas de boucles (arêtes reliant un sommet à lui-même) ni d'arêtes multiples (plusieurs arêtes reliant les mêmes sommets).
Exemples de graphes
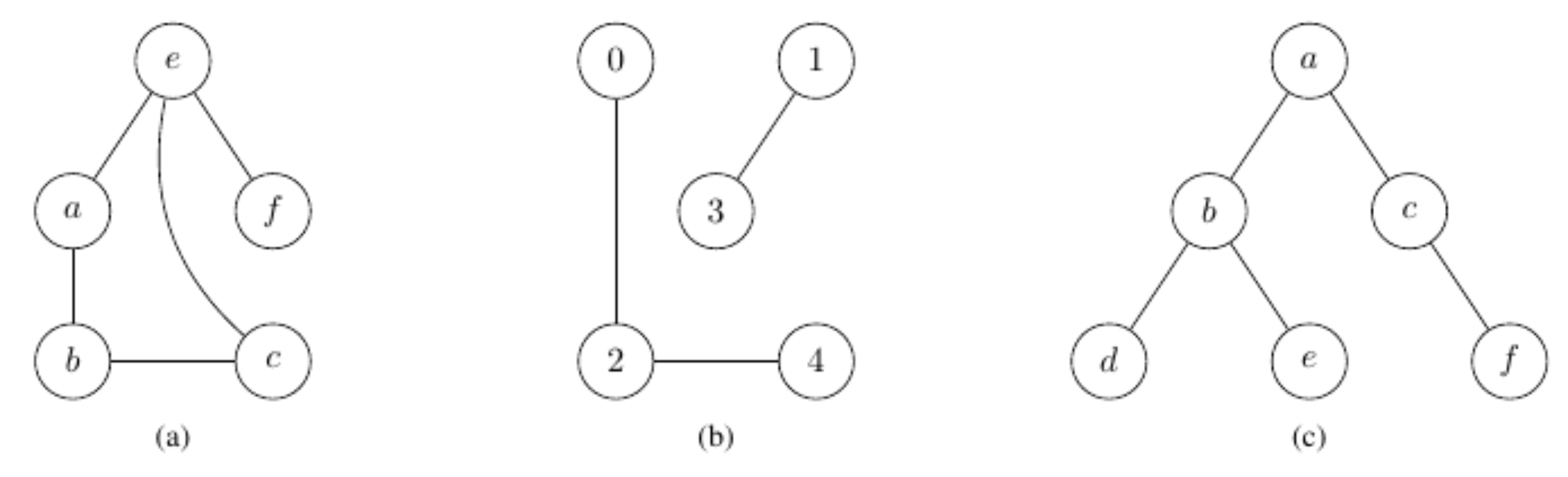
Exemple : Dans le graphe non orienté $G=(S,A)$ de la figure 2a, l'ensemble des sommets est $S=\{a,b,c,e,f\}$. et l'ensemble des arêtes est $A=\{(a,b),(a,e),(b,c),(c,e),(e,f)\}$. L'ordre du graphe est 5 et sa taille est 5. C'est un graphes simple.
À faire vous même
Décrire la structure du graphe de la figure 2b De la même façon que dans l'exemple. Quelle est la particularité de ce graphe ?
Décrire la structure du graphe de la figure 2c de la même façon que dans l'exemple. Quelle est la particularité de ce graphe ?
Vocabulaire
- Sommets adjacents : deux sommets sont adjacents s'ils sont reliés entre eux par une arête. On dit que l'arête est incidente aux deux sommets.
- Voisins d'un sommet $x$: ce sont tous les sommets reliés à par une arête.
- Degré d'un sommet $x$ : nombre d'arêtes incidentes au sommet, on le note $d(x)$.
Graphes orientés
Définition
Un graphe orienté est la donnée d'un ensemble $G=(S,A)$ où $S$ est un ensemble fini non vide dont les éléments sont appelés sommets et $A$ est un multi-ensemble fini de paires ordonnées d'éléments de $S$ appelées arcs.
Remarque
On parle d'arc et non d'arête pour un graphe orienté. La seule différence est que les arcs sont orientés, avec un sommet de départ et un sommet d'arrivé là où les arêtes n'ont pas de direction.
Propriétés
- Comme pour les graphes non orientés, le nombre de sommets est appelé ordre du graphe et le nombre d'arcs est appelé taille du graphe
- Les sommets sont représentés par des cercles et les arcs par des flèches.
- Un arc reliant un sommet à lui-même est appelé une boucle.
- Un arc partant d'un sommet $u$ et arrivant à un sommet $v$ est noté $(u,v)$
- Deux sommets peuvent être reliés par plusieurs arcs.
Exemples de graphes orientés
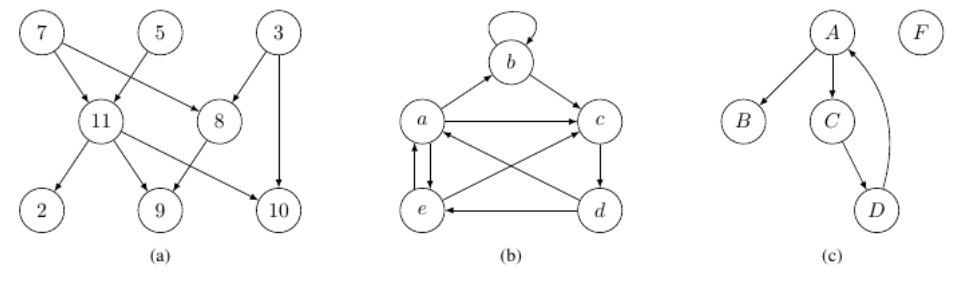
Exemple : Dans le graphe non orienté $G=(S,A)$ de la figure 3a, l'ensemble des sommets est $S=\{2,3,5,7,8,9,10,11\}$. et l'ensemble des arcs est $A=\{(3,8),(3,10),(5,11),(7,8),(7,11),(8,9),(11,2),(11,9),(11,10)\}$. L'ordre du graphe est 8 et sa taille est 9. C'est un graphes simple.
À faire vous même
Décrire la structure du graphe de la figure 3b De la même façon que dans l'exemple. Quelle est la particularité du sommet b ?
Décrire la structure du graphe de la figure 3c de la même façon que dans l'exemple. Quelle est la particularité du sommet F ?
Vocabulaire
- Sommets adjacents : Un sommet $u$ est dit adjacent à un sommet $v$ si $(u,v)$ appartient à $A$, c'est à dire s'il existe un arc allant de $u$ vers $v$
- Voisins d'un sommet $x$: ce sont tous les sommets reliés à par une arête ou un arc, quelque soit le sens.
- Degré d'un sommet $x$ : On appelle degré entrant d'un sommet le nombre d'arcs qui y arrivent, degré sortant d'un sommet le nombre d'arcs qui en partent et le degré est la somme du degré entrant et du degré sortant