Introduction

Image by Pete Linforth from Pixabay
Historique
Au début du XVIIIe siècle, la ville de Koenigsberg est traversée par la rivière Pregel. La ville est divisée en quatre quartiers par la rivière et ses deux affluents. La particularité de Koenigsberg est que la rivière est parsemée de sept ponts qui relient les quartiers entre eux. Les habitants de la ville se posent alors la question suivante : est-il possible de traverser chaque pont une seule fois et de revenir à son point de départ ?
Ce problème, appelé le problème des ponts de Koenigsberg, serait à l'origine de la théorie des graphes. En 1736, le mathématicien suisse Leonhard Euler démontre que le problème n'a pas de solution. Pour cela, il modélise la ville de Koenigsberg par un graphe, c'est-à-dire un ensemble de sommets reliés par des arêtes.
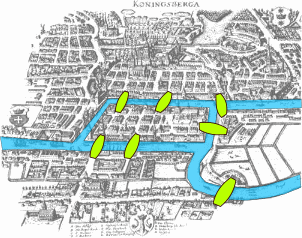
Les ponts de Königsberg
Par Bogdan Giuşcă — Public domain (PD),based on the image , CC BY-SA 3.0, Lien

Schématisation des ponts de Königsberg
Il démontre que pour qu'il soit possible de traverser chaque pont une seule fois et de revenir à son point de départ, il faut que chaque sommet du graphe soit de degré pair, c'est-à-dire que chaque sommet soit relié à un nombre pair d'arêtes.
la théorie des graphes
La théorie des graphes est une branche des mathématiques qui étudie les graphes, c'est-à-dire des structures composées de sommets reliés par des arêtes. Les graphes sont utilisés pour modéliser des situations concrètes comme le problème des ponts de Koenigsberg ou des situations abstraites comme les réseaux sociaux, les réseaux informatiques, les circuits électriques, etc.
Les graphes sont utilisés dans de nombreux domaines comme l'informatique, la biologie, la sociologie, la géographie, la physique, la chimie, etc. Ils permettent de modéliser des situations complexes et de résoudre des problèmes concrets.
Quelques exemples concrets d'utilisation des graphes.
Il est possible de modéliser les connexions entre les ordinateurs et le réseau Internet par un graphe. Chaque ordinateur est un sommet du graphe et chaque connexion entre deux ordinateurs est une arête du graphe.

Les réseaux sociaux comme Facebook, Twitter, LinkedIn, etc. peuvent être modélisés par un graphe. Chaque utilisateur est un sommet du graphe et chaque relation entre deux utilisateurs est une arête du graphe.

Les circuits électriques peuvent être modélisés par un graphe. Chaque composant du circuit est un sommet du graphe et chaque connexion entre deux composants est une arête du graphe.
Les réseaux de transport comme les réseaux routiers, les réseaux ferroviaires, les réseaux aériens, etc. peuvent être modélisés par un graphe. Chaque ville est un sommet du graphe et chaque route, voie ferrée, ligne aérienne, etc. est une arête du graphe.

Les molécules peuvent être modélisées par un graphe. Chaque atome est un sommet du graphe et chaque liaison entre deux atomes est une arête du graphe.

Les différents états d'un programme informatique peuvent être modélisés par un graphe. Chaque état est un sommet du graphe et chaque transition entre deux états est une arête du graphe. C'est le cas par exemple pour les jeux vidéos, les automates, les réseaux de Petri, etc.