Représentation des entiers relatifs

Rappel sur l'écriture binaire

Un ordinateur est une machine électromécanique qui fondamentalement n'est capable de stocker les informations que sous forme de 0 et de 1. Mais nous pouvons utiliser ces informations pour représenter un grand nombre de données. Nous avons vu que l'on pouvait écrire les nombres sous forme binaire en utilisant la base 2. Ainsi, en base 2, on représentait le nombre 13 par 1101 par exemple.

Le principe de la numération en base 10 (numération décimale) que nous utilisons quotidiennement est de regrouper ce que l'on compte par paquet de 10. Il peut y avoir de 0 à 9 éléments. Quand on en a dix, on obtient une dizaine. Il peut y avoir de 0 à 9 dizaines. Quand on a dix dizaines, cela fait une centaine. Et ainsi de suite avec les puissances successives de 10 (les milliers, les dizaines de milliers, les centaines de milliers, les millions, etc.)

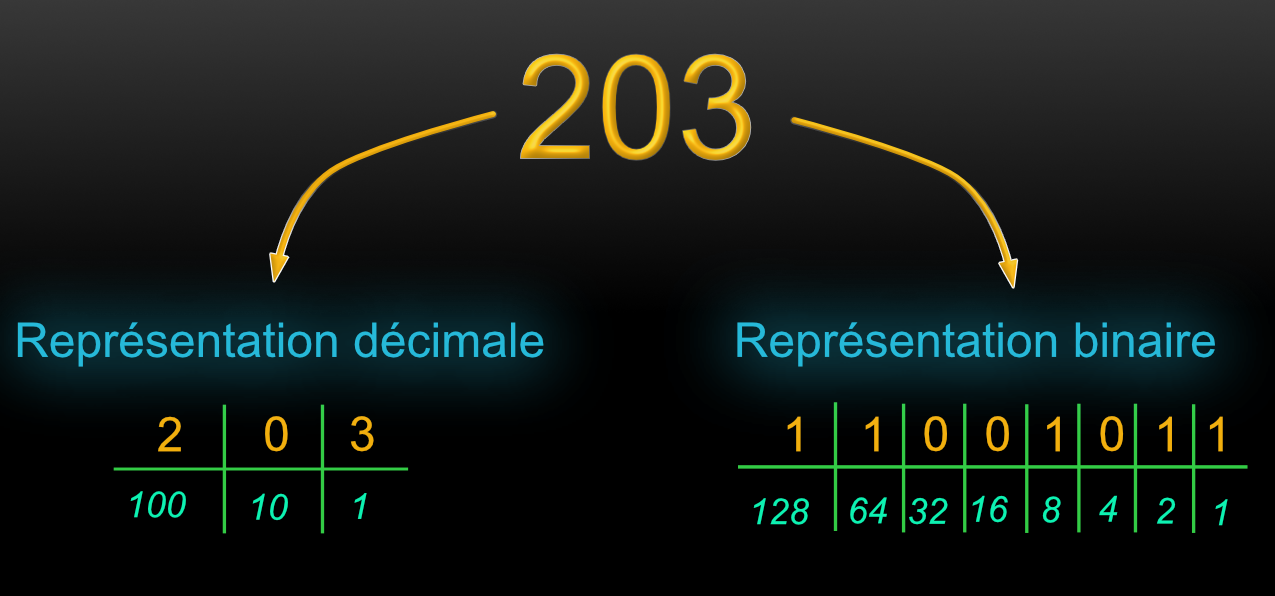
Ainsi, les nombres sont représentés en base 10 en utilisant des colonnes qui représentent les puissances successives de 10. Prenons par exemple 203. On peut écrire que \(203 =2\times 100 + 0 \times 10 + 3 \times 1 \), ou encore \(203 =2\times 10^2 + 0 \times 10^1 + 3 \times 10^0 \). On a la les puissances successives de 10 (\(10^0=1, 10^1 = 10, 10^2=100\)).

La numération binaire fonctionne de la même façon mais on fait des paquets dès que l'on a 2 éléments. On peut donc avoir 0 ou 1 élément. Si on en a deux, c'est un "paquet de 2" (une "deuzaine?"). Puis si on a 2 paquets de 2, on obtient un paquet de 4. Et ainsi de suite. On a donc à chaque fois 0 ou 1 unité, paquet de 2, paquet de 4, paquet de 8, paquet de 16, etc. On procède de la même façon de la même façon qu'en base 10, mais avec les puissances successives de 2.

Si nous reprenons l'exemple de 203 avec pour colonnes cette fois 1,2,4,8,16,32,64,128. On obtient \(203=1\times 128 + 1\times 64 + 1 \times 8 + 1 \times 2 + 1 \). Dit autrement, \(203=1\times 2^7 + 1\times 2^6 + 0 \times 2^5 + 0 \times 2^4 + 1 \times 2^3 + 0\times 2^2 +1\times 2^1 + 1\times 2^0 \). Donc, \(203_{10} = 1100\; 1011_2 \)

Nombres entiers relatifs

Maintenant comment faire pour représenter les nombres entiers relatifs ? Il ne faut pas oublier que l'on ne peut utiliser qu'une représentation binaire. De plus, ce serait bien d'avoir une représentation qui soit compatible avec ce que l'on a déjà fait pour les entiers positifs. Nous allons explorer les solutions qui s'offrent à nous.