Une autre approche
Approche en cycles
Dans une seconde approche, nous allons toujours coder les entiers en utilisant le bit de poids fort (c'est à dire le bit le plus à gauche) comme indiquant le signe, avec 0 pour les nombres positifs et 1 pour les nombres négatifs. Cependant, nous allons changer d'approche. Les 7 bits suivants ne contiendront pas la valeur absolue du nombre. Nous allons coder comme si nous étions revenus en arrière.
Pour toute cette partie, nous allons travailler sur des entiers codés sur 4 bits, afin de simplifier les schémas et les exemples. Le principe sera le même pour des entiers codés sur 8 bits (1 octet), ou sur 32 ou 64 bits (les tailles habituelles de codage des entiers dans beaucoup de langage). Si nous codons sur 4 bits, nous avons 16 possibilités. Si nous interprétons cela comme des écritures binaire, ce sont des nombres codés de 0 à 15.
Afin de rester compatible avec notre notation des entiers non signés, les entiers qui ont le bit le plus à gauche à 0 représentent la même chose que pour les entiers non signés. De 0 à 7, le codage reste donc le même.
Une fois que le bit de poids fort (le plus à gauche) est à 1, nous nous trouvons dans la partie des nombres négatifs. Mais nous allons continuer en partant de l'extrème gauche, donc de -15 si on travaille avec 4 bits. On obtient le schéma ci dessous, où l'on trouve en orange la représentation décimale qui correspondrait à l'entier non signé :

Une autre façon de représenter cela est de "replier" notre segment pour avoir les nombres les uns à la suite des autres :
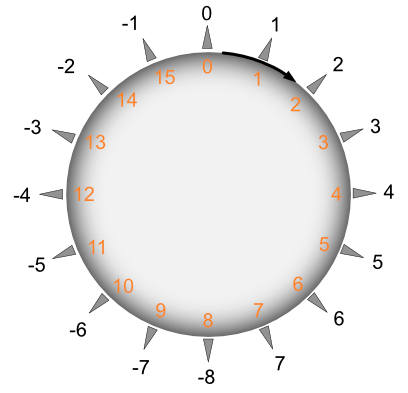
On peut donc donner le tableau de synthèse suivant :
| Notation binaire | valeur |
|---|---|
| 0000 | 0 |
| 0001 | 1 |
| 0010 | 2 |
| 0011 | 3 |
| 0100 | 4 |
| 0101 | 5 |
| 0110 | 6 |
| 0111 | 7 |
| 1000 | -8 |
| 1001 | -7 |
| 1010 | -6 |
| 1011 | -5 |
| 1100 | -4 |
| 1101 | -3 |
| 1110 | -2 |
| 1111 | -1 |
Intérêt de cette approche
En binaire, 15 s'écrit 1111. Le successeur en binaire est 1 0000. Si comme on est sur 4 bits, on peut dire que le successeur de 1111, c'est 0, car le 1 le plus à gauche est ignoré. Notre codage cyclique répond donc à deux idées :
- Les nombres dont le bit de poids fort est à 1 sont des nombres négatifs
- le successeur de -1 est 0
Regardons aussi comment fonctionne l'addition
Exemple
Calculons la somme de 4 et -3. 4 s'écrit 0100 et -3 s'écrit 1101 (cf tableau ci dessus). On aura l'addition suivante pour une addition bit à bit :
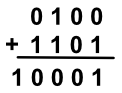
Comme nous sommes sur 4 bits, le 1 de gauche est ignoré. Nous avons donc pour résultat 0001, c'est à dire 1, ce qui est le bon résultat.
À faire vous même
Vérifiez qu'avec ce codage, l'addition bit à bit de -5 et de 5 donne bien 0
Dépassement de capacité
Il peut arriver que, dans l'additionneur n bits que nous utilisons, la dernière retenue nous donne 1 pour le chiffre de sortie. Si les deux nombres sont de signes contraire, ce n'est pas grave, ce 1 est ignoré. Si les deux nombres sont positifs ou si les deux nombres sont négatifs, cela signifie que l'on a dépassé la limite des 4 bits.
Complément à 2
Cette façon de représenter les nombres entiers relatifs sur n bit peut mathématiquement se résumer ainsi pour un entier k:
- Si \(0\leqslant k \lt 2^{n-1}\) on utilise la représentation binaire de k
- Si \(-2^{n-1} \leqslant k \lt 0\) on utilise la représentation binaire de \(2^n + k \)
Dit autrement, pour les négatifs, \(-k\) est codé par la représentation binaire de \(2^n - k \)
Cela s'appelle le complément à 2. Et l'avantage, c'est que c'est une opération très facile à faire bit à bit pour obtenir l'opposé d'un nombre. La technique est assez simple :
- On inverse tous les bits du nombres
- On ajoute 1
exemple
Prenons le nombre 5. Son écriture sur 4 bit est 0101.
- En inversant tous les bits, on obtient 1010
- En ajoutant 1, on obtient 1011
1011 est bien la représentation de -5.
À faire vous même
On considère des nombres entiers relatifs codés sur 8 bits (un octet). On peut donc représenter les nombres de -128 à 127. En utilisant la technique ci dessus, donner le codage de -5, de -45 et -68
- 5 s'écrirait 0000 0101. En inversant les bits, on a 1111 1010. En ajoutant 1, on obtient 1111 1011.
- 45 s'écrirait 0010 1101. En inversant les bits, on a 1101 0010. En ajoutant 1, on obtient 1101 0011.
- 68 s'écrirait 0100 0100. En inversant les bits, on a 1011 1011. En ajoutant 1, on obtient 1011 1100.
À retenir
Pour coder les nombres entiers relatifs sur n bits, on code les nombres entre 0 et \(2^{n-1}\) avec leur représentation binaire habituel. Pour coder leur opposé, on utilise le complément à 2 en inversant les bits et en ajoutant 1 au résultat.
Ce codage est compatible avec les additionneurs au niveau matériel.
Voici une vidéo qui reprend l'essentiel de ce chapitre :