Transistors et portes logiques
On entend souvent dire que l'informatique, ce n'est que des 0 et des 1. Dans les cours précédents, nous avons appris à compter en binaire, et vu avec le code ascii et le codage utf-8 que l'on pouvait représenter des chaînes de caractères avec des 0 et des 1. Nous allons voir que cette histoire de 0 et de 1 n'est pas qu'une lubie mathématique mais correspond aussi à une réalité physique. Par ailleurs, grâce aux travaux de BOOLE, on peut effectuer des opérations avec ces 0 et ces 1.
Le transistor et ses deux états
Lorsque l'on utilise des zéros et des uns, on se réfère en fait à un système qui peut avoir deux états. Ces états, que l'on choisit de nommer 0 et 1 pourraient aussi être appelés vrai ou faux (et on verra qu'il y a un lien). On peut aussi relier ces deux états à une réalité physique : un courant qui passe ou un courant qui ne passe pas (un interrupteur). Dans la pratique, les deux états que l'on utilise en informatique seront représentés par une tension dans le monde matériel. Par convention, l'état que l'on nomme 0 correspondra à une tension nulle, et l'état que l'on nomme 1 à une tension +V, fixée par le systèe utilisé.
Le tube à vide

Pentode EF86
Pour pouvoir avoir ces deux états, il faut disposer d'un interrupteur. Mais pour que le système soit intéressant, il ne faut pas un interrupteur mécanique, qui serait actionné par un être humain ou par un moteur. Il faut disposer d'un interrupteur controlé électriquement. Ainsi, le passage ou non d'un courant, la présence ou non d'une tension, sont controlés par un courant et on peut combiner tout cela pour faire des systèmes complexes.
Historiquement, la première technologie qui a permis cela était celle des tubes à vides, en particulier les triodes. Ces dispositifs à trois bornes avaient l'une des trois bornes qui jouait le rôle d'interrupteur électrique. Pour des raisons de stabilité et de perfomances, des bornes supplémentaires ont été rajoutées. La pentode est créée en 1926 par Bernard Tellegen de la société Philips.
Ces tudes à vide ont permis de créer les premiers ordinateurs. Jusqu'à l'avènement du transistor à la fin des années 40, les ordinateurs étaient des monstres de plusieurs tonnes (30 tonnes pour l'ENIAC!) qui occupaient des salles entières. Mais le principe est là : on a des interrupteurs controlés électriquement.
remarque
Si ces tubes ne sont plus utilisés aujourd'hui en informatique, on les trouve encore utilisés pour des traitements de haute fréquence et des amplificateurs de puissance, particulièrement dans le domaine de la HI-FI.
Les transistors
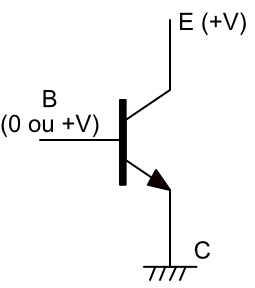
Schéma de principe du transistor
Les transistors que l'on trouve dans les circuits des ordinateurs se comportent comme des interrupteurs qui laissent passer ou non du courant électrique, selon un mode tout ou rien. Le schéma de principe donné ci contre montre les trois éléments caractéristiques du transistor :
- La base B. Lorsqu'elle est sous tension haute (+V), elle laisse passer le courant entre la broche E et le collecteur (relié ici à la masse). Ceci a pour effet de placer E sous tension basse
- La broche E est appelé l'émetteur, elle est reliée à l'alimentation +V du circuit. C'est en E que l'on mesure la tension de sortie.
- Le collecteurest lui relié à la masse
En pratique, des résistances font qu'il n'y a pas une tension nulle, pour éviter les courts-circuits, mais une tension très faible que l'on considère comme nulle.
Si l'on considère que la tension +V représente un 1 et la tension nulle représente un 0, ce transistor permet de faire une opération simple :
- Si l'entrée (B) est à 0, la sortie est à 1
- Si l'entrée est à 1, la sortie est à 0
Logique booléenne
Les travaux de Georges BOOLE au XIXème siècle visaient à rendre la logique calculable et démontrable. Il a ainsi créé une algébre (dite booléenne) qui travaille avec des 0 et des 1. Le 1 peut être considéré comme représentant VRAI et le 0 comme représentant FAUX. Les opérations de l'algébre booléenne sont ainsi les opérations de la logique classique.
Dans le cas de notre transistor, il réalise une opération élémentaire de la logique Booléenne qui est le NOT. En logique booléenne, on représente les opérateurs avec des tables de vérité. On parle de porte logique NOT, dont voici le schéma et la table de vérité

Porte NOT, notation américaine (ANSI) et européenne
| Porte NOT | |
|---|---|
| P | Q |
| 0 | 1 |
| 1 | 0 |
Portes logiques
Voici une vidéo qui présente de façon assez synthétique les constructions de portes logiques à partir de transistors